洁净室悬浮粒子浓度计算的统计学解释
根据《GBT16292-2010医药工业洁净室（区）悬浮粒子的测试方法》，悬浮粒子的计算分成4步：
第一步：采样点的平均悬浮粒子浓度A
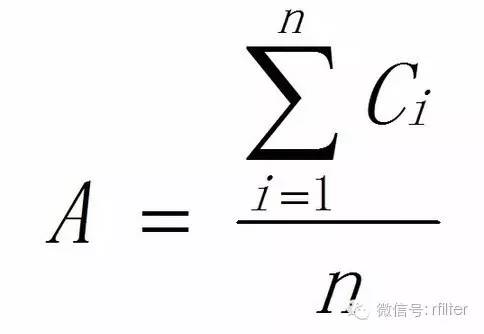
A——某一采样点的平均粒子浓度，粒每立方米（粒/m3）
Ci——某一采样点的粒子浓度（i=1,2,...，n），粒每立方米（粒/m3）
N——某一采样点上的采样次数，次。
统计学意义：通过对某个采样点多次重复采样，并通过求算术平均值的方式来消除随机误差，通常在实际检测中，连续采样检测3次
第二步：平均值的均值M
按公式:
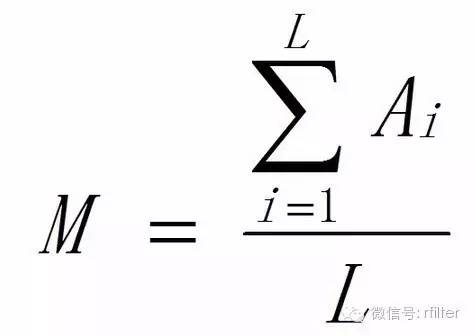
M——平均值的均值，即洁净室（区）的平均粒子浓度，粒每立方米（粒/m3）
Ai——某一采样点的粒子浓度（i=1,2,...，n），粒每立方米（粒/m3）
L——某一洁净室（区）内的总采样点数，个。
统计学意义：这步是为了计算出经过多个点多次采样的总平均值
第三步：标准差SE
按公式:
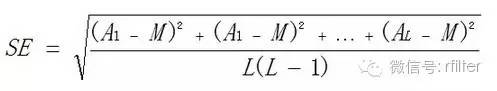
SE——平均值均值的标准误差，粒每立方米（粒/m3）
统计学意义:这步对于没有学过统计的同学可能理解上有些困难，我们把这个分成2步来理解。
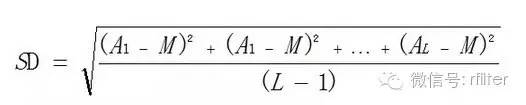
① 标准差
这个计算其实就是样本方差与总体方差的不同之处，我们通过选取几个采样点，并检测采样点的悬浮粒子浓度，以样本的情况来推断总体悬浮粒子的情况，所以我们应该用样本方差的公式来计算，
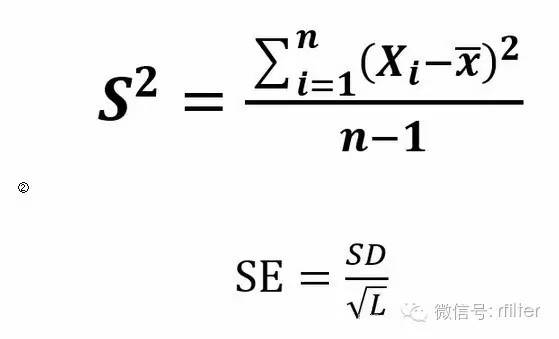
这步可以理解成，我们不断从一个总体（某个房间）中抽取样本量为L的样本（采样点）进行估计，那么这样总体和抽样后的结果（统计术语为样本均值的抽样分布）有什么关系呢，伟大的数学家直接给出了结论
即中心极限定理：
设从均值为μ、方差为σ^2;（有限）的任意一个总体中抽取样本量为n的样本，当n充分大时，样本均值的抽样分布近似服从均值为μ、方差为σ^2/n 的正态分布。
根据此定理我们得到样本均值的抽样分布的方差为总体方法的n分之一。换算成标准差即得到：
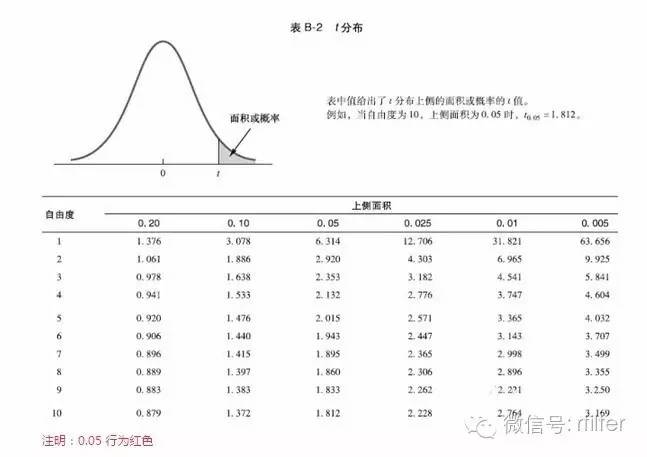
统计学意义：置信上限的计算在统计学中属于区间估计，因为在这里我们并不知道总体的方差，我们用样本方差来近似总体方差，只能认为分布情况适用t分布，而不是正态分布，这个需要大家注意，t分布自由度=L-1，所以我们看到上表中t的值与t分布表中颜色标注部分是一致的。
来源： 无尘无菌洁净室专家
整理：致众TACRO
【声明】部分文章和信息来源于互联网，不代表本订阅号赞同其观点和对其真实性负责。如转载内容涉及版权等问题，请立即与我们联系（杨 13260664005），我们将迅速采取适当措施
© 2018 - 2020, Wuhan Tacro Technology Co.，Ltd All Rights Reserved.
